Nguyên lý bảo mật tài khoản blockchain

- 13 mins
vietnam

Trong các bài viết trước, khi giới thiệu về công nghệ blockchain trong Bitcoin và Ethereum, mình đã có chia sẻ với các bạn là tài khoản (hay địa chỉ) đều được tạo ra bằng thuật toán, không cần kết nối mạng với bất kỳ một bên thứ 3 nào, điều này giúp đảm bảo sự bảo mật và ẩn danh tuyệt đối. Trong bài viết này, mình sẽ giới thiệu những nguyên lý bảo mật để xây dựng tài khoản trong blockchain, do hướng đến đối tượng bạn đọc phổ thông nên mình sẽ không đi quá sâu vào chi tiết kỹ thuật mà chỉ dừng lại ở những vấn đề cơ bản.

Mã hóa phi đối xứng

Có thể bạn đã từng đọc, nghe kể hoặc xem phim về nhà toán học Alan Turing trong hành trình giải mã cỗ máy Enigma của phát xit Đức, giúp cho phe Đồng Minh có thể giải mã được các tài liệu mật quan trọng, từ đó góp phần làm nên chiến thắng trong Thế chiến 2, đây là một ví dụ cực kỳ thực tế cho thấy tầm quan trọng của mã hóa bảo mật. Cỗ máy Enigma mã hóa tài liệu mà chỉ những người có khóa mới có thể giải mã, đây là kiểu mã hóa đối xứng tức là mã hóa và giải mã đều sử dụng chung 1 khóa. Loại mã khóa này có thiết kế đơn giản, tuy nhiên nó có một nhược điểm nguy hiểm là cần tất cả các bên tham gia đều phải nắm giữ và bảo vệ khóa, chỉ cần 1 bên sơ suất làm lộ khóa, toàn bộ tin mật sẽ bị lộ. Có một cách giải quyết đó là mỗi khóa chỉ được sử dụng để mã hóa thông tin giữa 2 người, tức là 1 người cần phải giữ khóa của những người còn lại, nhưng điều này làm cho việc quản lý và sử dụng khóa trở nên phức tạp khi số người tham gia tăng lên. Từ đây, một hệ thống mã hóa mới đã ra đời, được gọi là mã hóa phi đối xứng.

Mã hóa phí đối xứng có 1 cặp gồm 2 khóa, một khóa công khai (public key) và một khóa bí mật (private key). Khi tài liệu được mã hóa bằng Public key thì chỉ có Private key tương ứng mới giải mã được và ngược lại, khi mã hóa bằng private key thì chỉ có public key mới có thể giải mã. Tính chất này giúp giải quyết 2 vấn đề:

Tính chất thứ 2 của mã hóa phi đối xứng được ứng dụng để tạo ra chữ ký số. Bằng cách sử dụng một hàm băm trên tài liệu sẽ được 1 số 32 bytes (có ~ 78 chữ số trong hệ thập phân), hàm băm đảm bảo rằng bất kỳ thay đổi nào trong đầu vào cũng sẽ dẫn đến thay đổi kết quả băm, người gửi sau đó sẽ sử dụng private key của họ để mã hóa kết quả băm và tạo thành chữ ký (Signature), chữ ký sẽ được gửi kèm cùng với tài liệu đã mã hóa. Khi nhận được, người gửi sẽ tính toán lại giá trị băm của tài liệu, dùng public key của người gửi để giải mã chữ ký, nếu ra được kết quả băm => chữ ký được xác thực.

Thuật toán chữ ký số Schnorr

Trong bối cảnh blockchain, người ta sử dụng những thuật toán chuyên dùng để tạo và xác thực chữ ký số cho giao dịch, 2 thuật toán phổ biến nhất là Schorr và ECDSA. Trong đó Schorr là thuật toán mới hơn, hiệu suất tốt hơn khi hỗ trợ được đa chữ ký, đồng thời cũng đơn giản và dễ hiểu hơn ECDSA. Schorr đã được hỗ trợ trên Bitcoin kể từ nâng cấp Taproot (14/11/2021), còn ECDSA vẫn đang được sử dụng trên Ethereum và nhiều EVM blockchain khác. Cả 2 thuật toán đều dựa trên tính chất của đường cong Elliptic:

\[EC: y^2 = x^3 + ax + b\]

Trên đường cong này có tồn tại một phép cộng 2 điểm như sau: đường thẳng đi qua 2 điểm (A & B) không đối xứng trên đường cong sẽ cắt đường cong tại điểm thứ 3 (C), nếu lấy đối xứng điểm cắt này qua trục $Ox$ ta sẽ được điểm thứ 4 (D) cũng nằm trên đường cong là tổng của 2 điểm A&B.

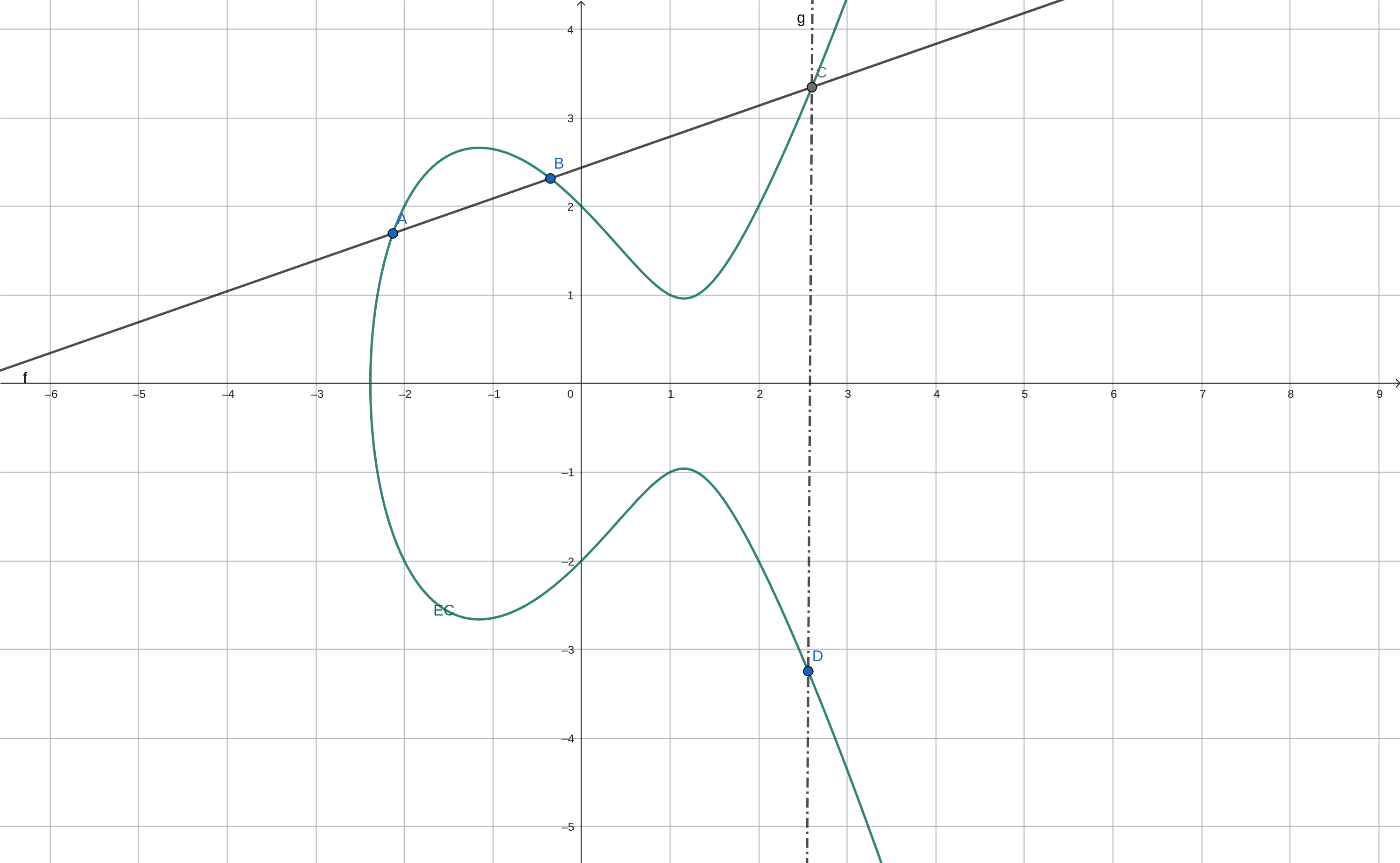
elliptic-curve

Nếu cho A trùng vào B (điểm P) ta sẽ được tiếp tuyến của đường cong, đường thẳng này cắt đường cong tại 1 điểm, lấy đối xứng qua $Ox$ ta sẽ được điểm 2P. Từ đây ta có một phép nhân 1 số với một điểm trên đường cong.

elliptic-curve

Như vậy từ 1 điểm $P$ ban đầu ta có thể dễ dàng xác định điểm $n.P$ với $n$ là một số nguyên. Tuy nhiên nếu biết 2 điểm $P$, $Q$ và biết $Q=n.P$ thì ta lại không thể có cách nào để tìm được n dễ dàng ngoài việc thử lần lượt các giá trị n!!! Đây được gọi là một phép toán 1 chiều và là cơ sở để xây dựng 2 thuật toán kể trên.

Tạo khóa

Quay trở lại với thuật toán Schorr, bộ khóa public key và private key được xây dựng từ công thức sau:

\[Q = x.G\]

Trong đó G là một điểm nằm trên đường cong EC được chia sẻ công khai (Các tham số của đường cong có thể lấy trong tài liệu chuẩn: SEC 2: Recommended Elliptic Curve Domain Parameters). $x$ là private key, một số được chọn ngẫu nhiên trong không gian số 32 bytes (64 số trong hệ hex16, ~78 số trong hệ thập phân). Q là public key, kết quả của phép nhân, cũng là 1 điểm nằm trên đường cong EC. Với không gian số của private key, việc dò được private key từ public key là điều không thể ở thời điểm hiện tại.

Ký giao dịch

Để ký giao dịch, thuật toán sẽ chọn ngẫu nhiên một số $k$ trong không gian số sau đó xác định điểm $R$

\[R = k.G\]

Tiếp theo là sử dụng hàm băm $H$ trên dữ liệu cần ký $m$:

\[e = H(R \,\|\, Q \,\|\, m)\]

Tạo chữ ký từ $e$:

\[s = k + e.x\]

Chữ ký được đính kèm giao dịch là:

\[\sigma = (R, s)\]

Xác thực

Từ phía Miner hoặc Validator để xác thực giao dịch chỉ cần kiểm tra đẳng thức sau:

\[s.G \stackrel{?}{=} R + e.Q\]

Đẳng thức này có thể dễ dàng chứng minh được khi bạn nhân G với công thức tạo signature:

\[s.G = k.G + e.x.G \Leftrightarrow s.G = R + e.Q\]

Lưu ý quan trọng: Tử huyệt của thuật toán Shnorr hay cả ECDSA nằm ở số ngẫu nhiên $k$ mỗi lần ký giao dịch, chỉ cần $k$ bị lộ trong giao dịch hoặc sử dụng trùng $k$ trong 2 giao dịch, lập tức private key $x$ sẽ bị lộ. Ngoài ra, nếu thuật toán chọn ngẫu nhiên số $k$ không đủ tốt (không đủ ngẫu nhiên trên toàn bộ không gian số) kẻ tấn công có thể thực hiện brute-force để tìm k trong không gian số bị giới hạn. Do đó cách tốt hơn là chọn k một cách xác định theo chuẩn RFC 6979:

\[k = H(x \,\|\, m)\]

Tạo ví bằng Hierarchical Deterministic wallet

Khi quản lý tài sản số trên Blockchain, chúng ta thường có nhu cầu sử dụng nhiều ví cho các mục địch khác nhau, để dễ dàng trong việc quản lý và bảo vệ các ví này HD wallet đã ra đời dựa trên 3 tiêu chuẩn được mô tả trong BIP-32, BIP-39, BIP-44. HD wallet cho phép người dùng tạo và quản lý vô hạn ví một cách dễ dàng, an toàn, có thể sao lưu và khôi phục ví khi cần. Với những ưu điểm như vậy, HD wallet đã trở thành tiêu chuẩn được implement trong nhiều ví phổ thông như Metamask, Ledger, Trust wallet, Electrum, Bitcoin core…

Trước khi HD wallet ra đời, thông tin khóa của các ví được lưu trữ trong các thiết bị nhớ như ổ cứng, usb…, đối mặt với nguy cơ mất mát hỏng hóc, do đó người dùng thường xuyên phải sao lưu định kỳ để đảm bảo an toàn. Ở HD wallet, thay vì các ví được sinh ra ngẫu nhiên chúng được phát triển từ một hạt giống (master seed) thông qua một thuật toán xác định được mô tả trong BIP-32.

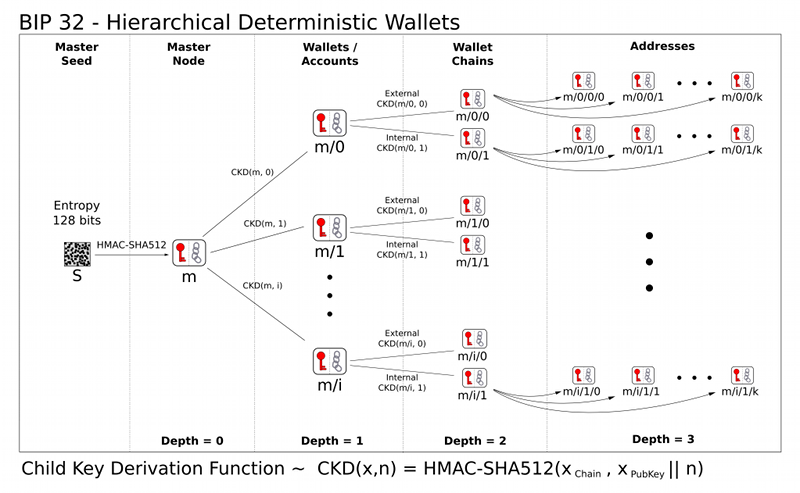
HD wallet

Theo cách này, vô số ví có thể được tạo ra chỉ từ 1 Seed ban đầu mà vẫn giữ nguyên được sự bảo mật như một ví được tạo ngẫu nhiên. Mỗi ví là kết quả của việc biến đổi seed theo một đường dẫn (path) duy nhất, và để cho việc này trở nên xác định hơn nữa, tiêu chuẩn BIP-44 sẽ quy định cụ thể về các path này để người dùng không cần phải nhớ về chúng. Người dùng chỉ cần nắm giữ master seed là có thể khôi phục lại toàn bộ các ví gắn với master seed đó. Dưới đây là các bước để tạo ra master seed (hoàn toàn offline trên thiết bị):

Ví nóng, ví lạnh, ví đa chữ ký

Cách để phân biệt ví nóng và ví lạnh là dựa vào nơi mà Private key của nó được lưu trữ. Nếu Private key nằm trong một thiết bị được kết nối internet, thường là các phần mềm trên máy tính, điện thoại thì đó là ví nóng. Ưu điểm của ví nóng là tiện lợi, dễ sử dụng, dễ tích hợp nhưng sẽ rất nguy hiểm nếu thiết bị không an toàn, nhiễm virus hoặc bị theo dõi, vì vậy ví nóng chỉ thích hợp để chứa tài sản nhỏ, ngắn hạn và sử dụng hàng ngày.

Khác với ví nóng, ví lạnh bảo vệ Private key của nó trong một môi trường cách ly hoàn toàn với Internet, thường là thiết bị giống như USB hoặc thẻ cứng có chíp xử lý riêng. Khi thực hiện giao dịch, thông tin giao dịch sẽ được gửi vào thiết bị, tại đây chíp xử lý của thiết bị sẽ sử dụng Private key của ví để tạo chữ ký cho giao dịch, chữ ký sau đó sẽ được trả về cho thiết bị yêu cầu để thực hiện tiếp giao dịch. Toàn bộ quá trình này, Private key không rời khỏi thiết bị nên đảm bảo an toàn tuyệt đối.

Khi sử dụng ví lạnh thì bạn cần phải tự bảo quản thiết bị của mình, nếu xảy ra hỏng hóc hoặc bị mất, bạn sẽ không thể khôi phục lại được. Đa số ví lạnh hiện nay đều không cho phép lấy Private key hay Seed phrase ra từ thiết bị dù là để backup, điều này giúp đảm bảo nguyên tắc Private key không bao giờ rời khỏi thiết bị nhưng lại biến ví lạnh trở thành một điểm chết duy nhất.

Để tránh những rủi ro với ví lạnh, đối với những tài sản lớn và quan trọng, người ta thường kết hợp với ví đa chữ ký, đây là loại ví yêu cầu có nhiều hơn 1 chữ ký mới có thể thực hiện giao dịch, ví dụ 1 ví đa chữ ký 2/3 sẽ yêu cầu có 2 trong 3 chữ ký để thực hiện giao dịch. Như vậy khi kết hợp cùng ví lạnh sẽ đảm bảo rằng nếu 1 ví gặp vấn đề thì vẫn có thể sử dụng 2 ví còn lại để lấy lại tài sản.

Kết luận

Như vậy trong bài viết này mình đã giới thiệu với các bạn những nguyên lý cơ bản và các thuật toán bảo mật tài sản trên Blockchain, hẹn gặp lại trong các bài viết sau!

Related Posts